This is a collection of geometry problems that I maintain for myself and others and a shrine to Euclidean Geometry as a whole.

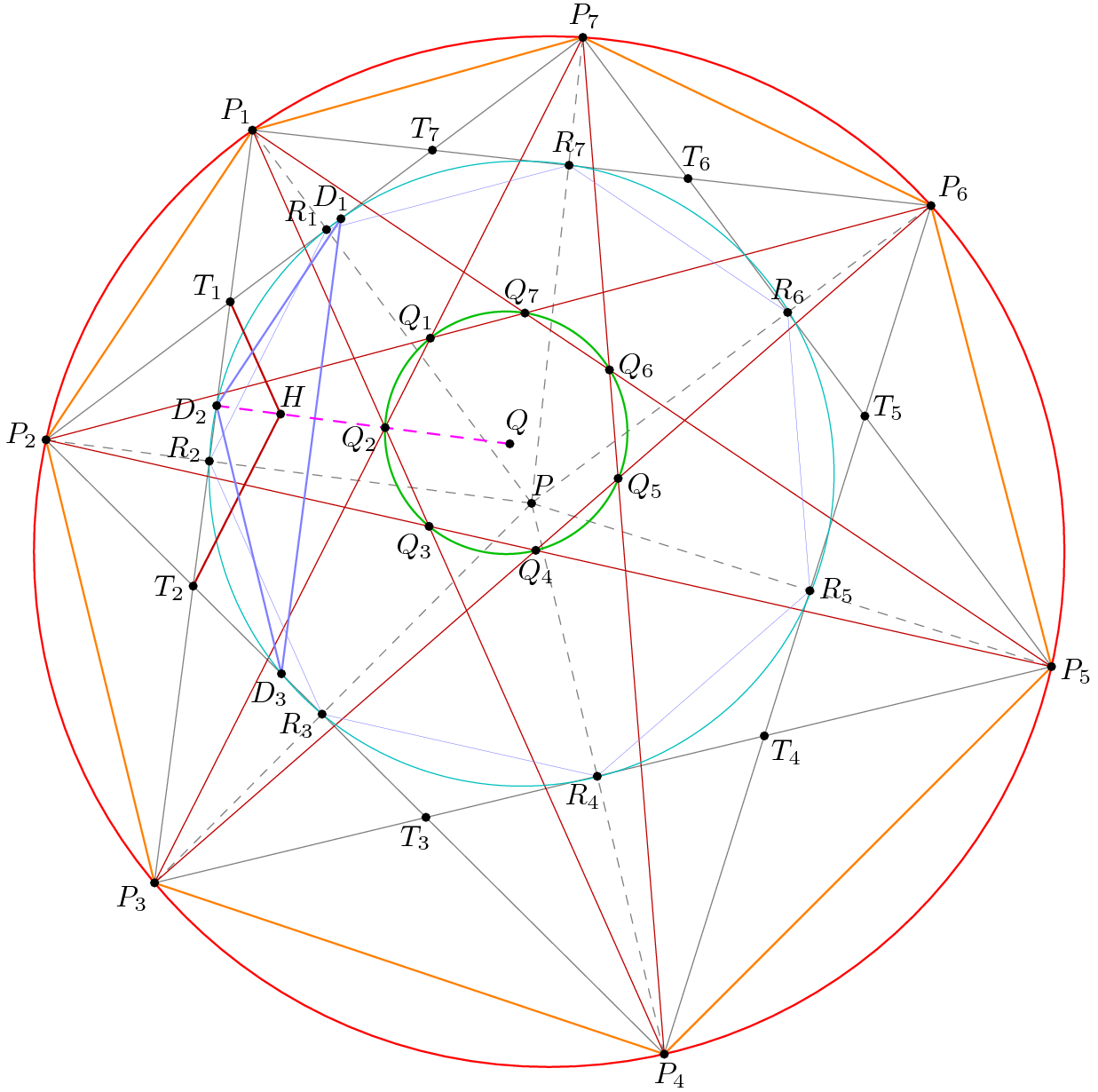
The diagram above is from the 2020 USA Team Selection Test, which determined the contestants who competed in the International Mathematical Olympiad for the USA team. It is problem number 6, the final problem, and perhaps the most elegant geometry problem to appear on an Olympiad. Of the hundreds of contestants who attempted the problem, not a single contestant earned a single point out of the maximum of 7.
This is a list of documents arranged by difficulty containing geometry problems. Unless otherwise noted, the problem is either original or classical. This list is currently recieiving updates, and more problems are added when the website is updated.
Most of these problems can be solved by an exceptional honors student and although some are difficult, not much mathematical reasoning or problem solving is required. The depth of these problems is fairly shallow, and less than 100 hours of geometry training will more than suffice.
These problems require more geometry experience and need far more thought. No honor student without some exposure to Euclidean Geometry in mathematical contests is capable of solving these. The depth of the problems have increased and problems require problem solving from multiple areas of geometry to solve the problems. No problem in this group can be solved simply by knowing a formula or making a single observation.
These are the most difficult problems in competition math, often inspired by Olympiad contests. Some may take hours to solve, and key observations which can only be made after hundreds of hours of geometry experience. The depth of these problems is very deep, and an honor student would make no progress whatsoever with regular mathematical problem solving skills. Despite being the most difficult, however, they tend to be the most elegant.